| syntax |
level |
semantics |
| expr , expr |
0 |
creation of a vector from x and y components |
| expr or expr |
1 |
logical or |
| expr and expr |
2 |
logical and |
expr = expr
expr == expr |
3 |
equal |
expr <> expr
expr != expr |
3 |
not equal |
| expr < expr |
3 |
less than (x component is dominant) |
| expr <= expr |
3 |
less than or equal (x component is dominant) |
| expr > expr |
3 |
greater than (x component is dominant) |
| expr >= expr |
3 |
greater than or equal (x component is dominant) |
| expr dot expr |
4 |
vector dot product |
| expr cross expr |
4 |
vector cross product |
| expr + expr |
5 |
addition |
| expr - expr |
5 |
subtraction |
expr expr
expr * expr |
6 |
complex multiplication |
| expr / expr |
6 |
complex division |
| expr rem expr |
6 |
remainder (on the x component only) |
| expr mod expr |
6 |
modulo (on the x component only) |
| expr ^ expr |
7 |
complex power |
| + expr |
8 |
(the identity operator) |
| - expr |
8 |
complex negation |
| not expr |
8 |
logical not |
| re expr |
8 |
extraction of the x component |
| im expr |
8 |
extraction of the y component (as a real value) |
| realonly expr |
8 |
the value of expr, but undefined unless expr is real |
| int expr |
8 |
truncate to integer (independently on both x and y) |
| ceil expr |
8 |
ceiling integer (independently on both x and y) |
| floor expr |
8 |
floor integer (independently on both x and y) |
| sign expr |
8 |
the sign of expr, or its collinear unit vector |
| abs expr |
8 |
complex absolute value, or vector length |
| arg expr |
8 |
complex argument, or vector angle |
| conj expr |
8 |
complex conjugate |
| sqrt expr |
8 |
complex square root |
| exp expr |
8 |
complex exponential eexpr |
log expr
ln expr |
8 |
complex natural logarithm |
| sin expr |
8 |
complex sine |
| cos expr |
8 |
complex cosine |
| tan expr |
8 |
complex tangent |
| cot expr |
8 |
complex cotangent |
| sec expr |
8 |
complex secant |
| csc expr |
8 |
complex cosecant |
| sinh expr |
8 |
complex hyperbolic sine |
| cosh expr |
8 |
complex hyperbolic cosine |
| tanh expr |
8 |
complex hyperbolic tangent |
| coth expr |
8 |
complex hyperbolic cotangent |
| sech expr |
8 |
complex hyperbolic secant |
| csch expr |
8 |
complex hyperbolic cosecant |
asin expr
arcsin expr |
8 |
complex inverse sine |
acos expr
arccos expr |
8 |
complex inverse cosine |
atan expr
arctan expr |
8 |
complex inverse tangent |
acot expr
arccot expr |
8 |
complex inverse cotangent |
asec expr
arcsec expr |
8 |
complex inverse secant |
acsc expr
arccsc expr |
8 |
complex inverse cosecant |
asinh expr
arcsinh expr |
8 |
complex inverse hyperbolic sine |
acosh expr
arccosh expr |
8 |
complex inverse hyperbolic cosine |
atanh expr
arctanh expr |
8 |
complex inverse hyperbolic tangent |
acoth expr
arctoth expr |
8 |
complex inverse hyperbolic cotangent |
asech expr
arcsech expr |
8 |
complex inverse hyperbolic secant |
acsch expr
arccsch expr |
8 |
complex inverse hyperbolic cosecant |
| expr . x |
9 |
extraction of the x component |
| expr . y |
9 |
extraction of the y component (as a real value) |
| ( expr ) |
9 |
definition of a subexpression |
| | expr | |
9 |
complex absolute value, or vector length |
| number |
|
a real number value, or the vector (number,0) |
| i |
|
the complex number V¯-1, or the vector (0,1) |
| j |
|
the complex number V¯-1, or the vector (0,1) |
| pi |
|
the real number 3.14159265358979324 |
| e |
|
the real number 2.71828182845904524 |
| infinity |
|
the infinity value (example: the result of 1/0) |
| NaN |
|
the "Not a Number" value (example: the result of 0/0) |
| a |
|
the value of point a (a complex or vector value) |
| ax |
|
the x component of point a (a real value) |
| ay |
|
the y component of point a (a real value) |
| b |
|
the value of point b (a complex or vector value) |
| bx |
|
the x component of point b (a real value) |
| by |
|
the y component of point b (a real value) |
| c |
|
the value of point c (a complex or vector value) |
| cx |
|
the x component of point c (a real value) |
| cy |
|
the y component of point c (a real value) |
| d |
|
the value of point d (a complex or vector value) |
| dx |
|
the x component of point d (a real value) |
| dy |
|
the y component of point d (a real value) |
| f |
|
the expression defined by function f |
| fx |
|
the x component of function f |
| fy |
|
the y component of function f |
| g |
|
the expression defined by function g |
| gx |
|
the x component of function g |
| gy |
|
the y component of function g |
| h |
|
the expression defined by function h |
| hx |
|
the x component of function h |
| hy |
|
the y component of function h |
| k |
|
the expression defined by function k |
| kx |
|
the x component of function k |
| ky |
|
the y component of function k |
| m |
|
the expression defined by function m |
| mx |
|
the x component of function m |
| my |
|
the y component of function m |
| n |
|
the expression defined by function n |
| nx |
|
the x component of function n |
| ny |
|
the y component of function n |
| x |
|
the value of the autoplot variable (a real value) |
| t |
|
the value of the autoplot variable (a real value) |
| s |
|
the value of the step variable (an integer value) |
| z |
|
the value of the current zoom scale (an integer value) |
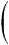
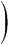
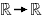
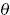
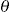
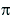 >
>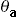 ) * (|b| ei
) * (|b| ei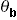 )
)