RELAZIONE DI FISICA
Nomi Alunni: Data: 17/01/2002.
Titolo Esperienza: Densità di un solido regolare
Obbiettivi dell’esperienza:
Imparare ad usare gli strumenti di misura (calibro a nonio ventesimale);
Determinare il volume di un solido;
Determinare la sua massa;
Calcolarne la densità.
Materiale occorrente:
Parallelepipedo di metallo;
Calibro a nonio ventesimale (s= 0.05mm);
Bilancia di precisione digitale (p: 2000g; s: 1g);
Tempo impiegato: 2 ore
Schema dell’esperienza:
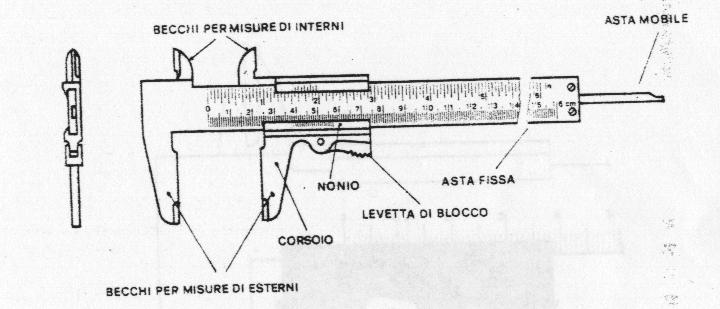
Procedimento:
Si sono misurate le tre dimensioni del parallelepipedo di metallo tramite il calibro a nonio ventesimale, quindi si è determinata la massa tramite la bilancia di precisione digitale. Si è proceduto al calcolo prima dell’area di una delle facce del parallelepipedo, poi al calcolo del volume, con il rispettivo errore assoluto, relativo e percentuale. Quindi si è fatto i rapporto tra massa e volume determinando così la densità, della quale si è calcolato il rispettivo errore assoluto, relativo e percentuale.
Tabella dei dati raccolti:
Dimensioni del solido: a=(58.40 ± 0.05) mm; b=(25.00 ± 0.05)mm; c=(3.00 ± 0.05)mm
Massa del solido: m=(34 ± 1) gr
Elaborazione dei dati raccolti: