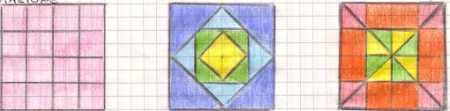
Esempi di figure equiscomponibili simmetriche rispetto alla rotazione
SCUOLA MEDIA STATALE "GIULIANO DA SANGALLO"
EQUISCOMPONIBILITA'
Esempi di figure equiscomponibili simmetriche rispetto alla rotazione

Inoltre se in una superficie piana (ad esempio un rettangolo), formata da figure equiscomponibili, io cambiassi la composizione e la posizione di quelle figure, la superficie piana rimarrebbe, in tutti i casi invariata.
Esempi di figure equiscomponibili e asimmetriche rispetto alla rotazione
Prima:  Dopo:
Dopo: 
Prima:  Dopo:
Dopo: 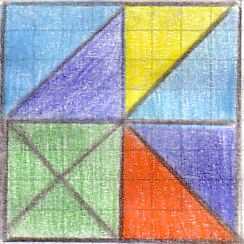
L'equivalenza tra figure piane vuol dire che queste hanno la stessa area, cioè la stessa superficie anche avendo diverse forme; inoltre scomponendo una figura piana in altre figure geometriche al suo interno e ordinandole in un diverso modo tra loro si forma un'altra figura, questa proprietà si chiama equiscomponibilità:
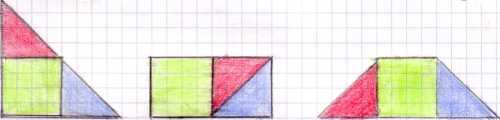

Due figure quindi sono equivalenti quando, anche essendo due figure piane differenti, hanno la stessa area, questo solo con le figure piane perchè quelle solide per essere equivalenti non avrebbero più la stessa area ma lo stesso volume.
Fate il calcolo dell'area di queste due figure:
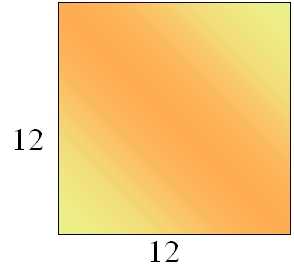


Come potete notare dalle immagini io ho spostato solo le figure nell'area dello stesso quadrato ed ho così dimostrato che queste due figuresono equiscomponibili. Questo è solo un esempio, perchè questa stessa operazione può essere fatta su altre figure geometriche piane e con altri motivi disegnati nelle aree delle figure.