 |
 |
 |
 |
|
 |
SCUOLA MEDIA STATALE "GIULIANO DA SANGALLO"
UNA SCUOLA SUPERIORE CI VIENE IN AIUTO
 |
 |
 |
 |
|
 |

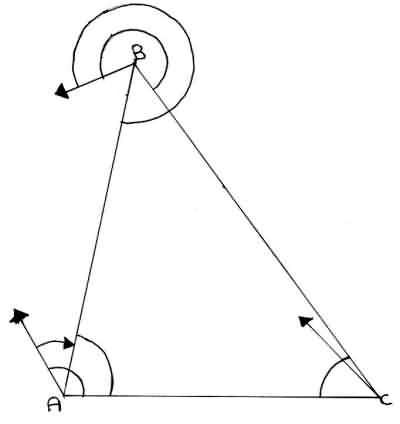
| A | B C |
67,134 149,370 |
Angolo BAC = 149,370° - 67,134° = 82,236° |
| B | A C |
356,496 301,222 |
Angolo ABC = 356,496° - 301,222° = 55,274° |
| C | A B |
347,718 10,214 |
Angolo ACB = 347,718° - 10,214° = 337,504° a questo punto 400° - 337,504° = 62,496° |
| A questo punto: |
|
||